전세계 시장이 지켜보고 있는 지표가 하나 있다. 바로 미 국채 금리인데 요즘 미 국채 금리가 1.5%를 넘어가면서 그 영향으로 미국을 비롯해 전세계의 증시가 충격을 받고 있는 상황이다. 이런 혼란 속에서 이게 도대체 뭐라고 내 주식 가격을 떨어뜨리는가를 논하기 전에 금리가 올라가는데 채권 가격은 떨어진다는 게 무슨 말인지부터 짚고 넘어가고자 한다.
우리의 머릿속
우선, 우리가 통상 이해하고 있는 금리와 여기서 논하는 금리는 의미가 다르다. 우리의 머리 속에 들어와 있는 개념은 아래와 같다. 100,000원을 104,040원으로 만드는 방법 중 하나는 적금을 이용하는 것이다.

우리가 생각하는 일반적인 금융거래에서 수익률, 금리, 이자율을 떠올리면 금리가 올라가면 이자로 받을 수 있는 금액이 늘어나는 게 맞다. 그렇다면 채권의 경우는 어떨까

여기서부터 혼란이 찾아온다. 똑같은데 뭐가 잘못된거지? 용어정리가 필요하다.
두 가지의 금리
위의 두 가지 표에서 '연 2%짜리'라고 하는 부분은 표면금리/표면이율/발행이율/쿠폰금리 등으로 불리는 금리이다. 채권에게는 금리가 하나 더 있다. 채권수익률(국채수익률, 국채금리)/시장수익률/만기수익률/유통수익률이 그것이다.
채권에게만 두 가지 금리가 있는 이유는 채권은 거래가 가능하기 때문이다. (통장은 거래하면 감옥간다) 위에서 보았듯이 채권은 발행하면서 정해진, 변하지 않는 고정금리가 있어서 그대로 보유하고 있으면 2년 뒤에는 발행이율에 의해서 104,040을 받을 수 있다. 하지만 이를 보유하던 투자자가 1년 10일이 지난 시점에 중간지급된 이자도 이미 받은 상태로 이를 팔고 싶을 때 채권거래시장(유통시장)에서는 어떤 가격으로 팔아야 하는가를 생각할 때는 채권수익률 개념이 등장한다.
조금 더 어렵게
중고등학교 수학 시간에 배웠겠지만 연복리 이자율이 r이고 지금 원금이 P, 기간이 n년일 때 미래에 받을 금액 S는 다음과 같다.
$S\ =\ \combi{P\ \times \ \left(1+r\right)}^n$S = P × (1+r)n
이 식은 처음 예로 들었던 은행적금과 채권보유에 해당하는 경우이고 채권을 거래하게 되면 다음과 같이 정해져 있는 미래의 만기상환금으로부터 현재의 값을 추정하는 과정이라 생각하면 된다. (R은 만기수익률) 그래서 현재가격인 채권가격 P는 R(만기수익률 또는 국채금리)가 증가하면 분모가 증가하여 가격이 내려가는 것이다.
$P\ =\ \combi{\frac{S}{\combi{\left(1+R\right)}^n}}$P = S(1+R)n
그림으로 쉽게 정리하며 마무리
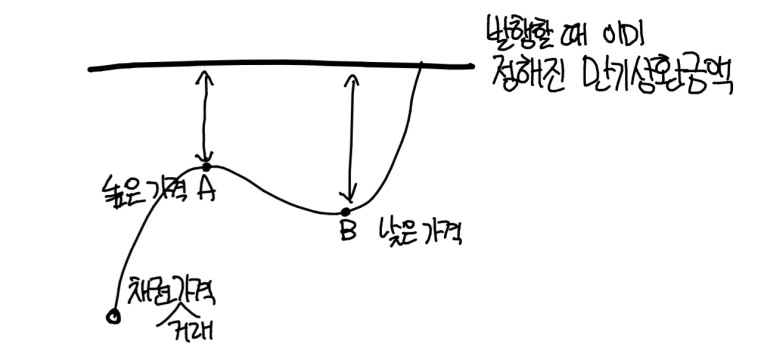
위의 그림에서 보듯 만기상환금액은 채권을 발행할 때 "이 채권은 발행가가 얼마이고 고정금리가 얼마이며 이는 얼마 주기로 지급이 되고..."의 형태로 미리 정해지기 때문에 언제 사든(물론 이표채처럼 이자를 주기적으로 지급하면 식이 더 복잡) 끝은 정해져 있다. 그러므로 내가 지금 거래를 하여 채권을 매수함으로써 얻을 수 있는 기대 수익은 얼마에 샀느냐에 따라 달라진다.
위의 A점은 가격이 높기 때문에 최종 기대 수익과 가까워서 화살표가 짧다.(만기수익률이 작다.) 반면, B는 낮은 가격에 매수하는 것이기 때문에 최종 기대 수익과 차이가 커 화살표가 크다.(만기수익률이 크다.) 결론을 정리하자면 통상적으로 뉴스 기사에 등장하는 채권의 금리는 만기수익률을 의미한다. 최종금액이 정해져 있는 채권 거래의 특성상 "지금 사면 매수금액 대비 몇 %의 이익이 확정!" 의 의미이기 때문에 채권금리와 가격은 반대로 움직인다.
'투자일기 > 투자 기본 개념' 카테고리의 다른 글
| 돌아오는 배당의 계절, 배당 받으려면 언제 사야 하나요? (배당락전일, 배당락일, 배당기준일, 배당기산일 정리) (0) | 2021.03.26 |
|---|---|
| ETF란 무엇인가? 불안한 한국 증시, 안정적인 ETF로 갈아타자 (3) | 2021.02.19 |
| 주식에서 오는 스트레스, MDD의 뜻 (1) | 2021.02.06 |



댓글